Trick Or ReTreat: Building a Custom Environment - Phase 2 🍬

Having successfully built and trained an agent in a simple environment with a single reward structure, the next step was to add more rewards to the environment. In this post, I will walk through the changes I made to my custom environment to include the extra rewards- ghosts and candies.

I’ll also explain the concept of Q-learning, how I implemented it to train the agent and share a video of the agent’s performance after training.

Reframing the Agent’s Objective

In Phase 1, the agent’s task was simple; find and reach the exit door. But now, with the addition of ghosts and candies, the agent not only needs to find and reach the exit, but also:

Avoid the ghosts
Collect as many candies as possible

Environment Features:

Both candies and penalties remained static throughout this phase.
There are 4 actions the agent can take: up, down, left and right.
The game terminates when the agent has reached the exit door of the haunted mansion.
Small penalty is applied for each step taken that does not result in termination (reaching the exit door).

Reward Logic:

The reward logic is now more complex:

Exit Door: Reward of + 20 for reaching the exit door and completing the task.
Candies: Reward of + 15 for each candy collected.
Ghosts: Penalty of -25 is given if the agent contacts a ghost. This high penalty ensures that avoiding ghosts is prioritised in Q-learning, where future rewards are considered. As a result, the penalty had to be higher than the target reward +20.(More on Q-learning later in the post).
Step Penalty: A small penalty of 0.01 for each action that doesn’t lead to the target. This penalty is set low to avoid discouraging exploration, which is needed during the early stages of Q-learning.

Custom Environment Updates

To add the ghosts and candies into the environment, I made the following changes to these methods of my environment class:

1). `init`: Initialising the Environment

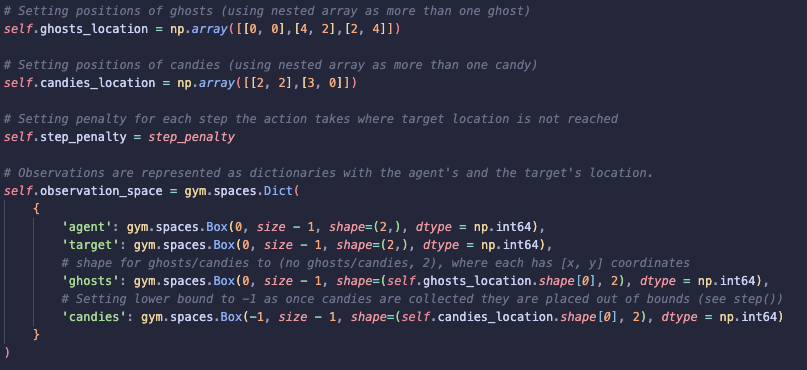
Adding the ghosts and candies to the environment, specifying their coordinates.
For Phase 2, all ghosts and candies are static and the agent is the only moving part in the environment.

2). `step`: Updating Environment After Action is Taken

Updated the reward logic to include penalty for encountering a ghost and reward for finding a candy.
Adjusted the reward structure since I was using Q-learning. This is because Q-learning considers both immediate rewards and future rewards and so, I needed to increase the penalty for encountering a ghost so that it outweighs the reward for reaching the target (door).
Similarly, I increased the reward for collecting candies to incentivise the agent to try and collect as many candies as possible.
Once a candy is collected by the agent, it is removed from the environment by setting its position out of bounds [-1,-1]. This prevents the agent from repeatedly collecting the same candy and avoiding the target. Without this step, the agent could get stuck in an infinite loop, collecting the same candy without ever finishing an episode.

3). `reset`: Resetting the Environment

Ensure candies are placed back in the environment at the start of each new episode.

4)_get_obs: Return State of Environment

Added location of the ghosts and candies to observations.

5). `render`: Visualising the Environment

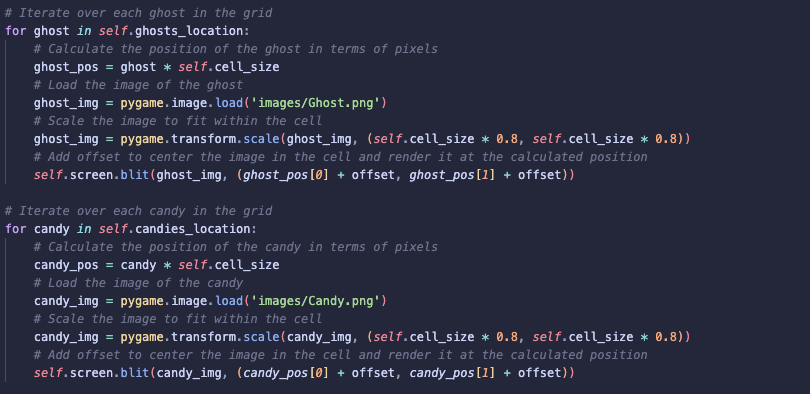
Added in ghosts and candies to the visualisation using images from Canva.

Note: I’ve only included code snippets for the parts of the environment where I made changes. For the full methods of the class, please refer to my GitHub repository for the Trick Or Treat project (to be uploaded on completing the project).

Training with Q-learning

In this section, I share how I trained the agent using Q-learning. While I also implemented PPO for comparison, this blog post will focus only on Q-learning. For a comparison between Q-learning and PPO, you can visit my GitHub to access notebooks.

Recap of Reinforcement Learning (RL)

RL is a type of machine learning where an agent learns to make decisions based on interactions with its environment. The agent learns through feedback on the actions it takes, updating its policy to maximise total rewards per episode.

Since the environment is more complex, I thought it best to use Q-learning to train the agent. Q-learning is a type of Temporal Differencing learning where updates occur after each step allowing real-time learning.

Let’s take a closer look at Q-learning to see how it works and how it can be implemented!

What is Q-learning?

Q-learning is a type of reinforcement learning where, instead of learning a policy, the agent builds a Q-table. This table stores Q-values which represent the ‘goodness’ of taking a particular action from a given state, based on the expected rewards. Over time, the agent updates these Q-values through its observations, gradually improving its ability to make decisions.

What makes Q-learning different is that it doesn’t just focus on immediate rewards, it also takes into account potential long-term rewards that can occur as a result of the agent taking an action. This concept confused me a little to start with, so let’s walk through an example to make it clearer:

Imagine a 2 by 2 grid environment.

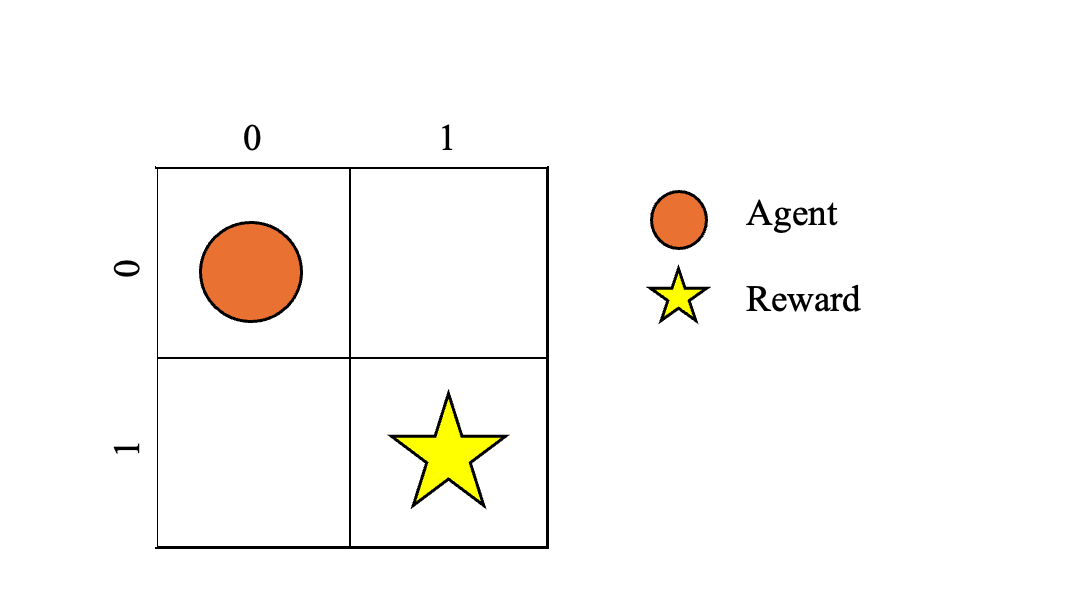
The agent can only take 4 actions: up, down, left, or right.
The agent’s goal is to reach the target (1,1). Once it reaches the target, the agent receives a reward and completes the task.
Assume the agent starts at (0,0).

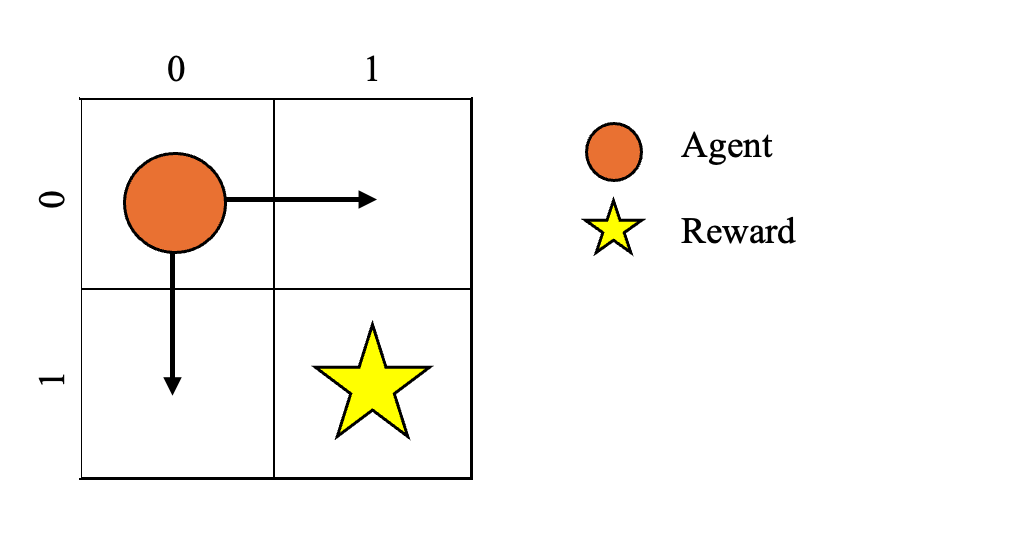
If the agent moves down from (0,0), it reaches (0,1). While there’s no immediate reward for this move, it’s a step closer to the target. As a result, the Q-value for moving down from (0,0) will increase because the state (0,1) has the potential for high future rewards.

Similarly, moving right from (0,0) leads to (1,0), which is also closer to the target. The Q-value for this action will also increase due to the possibility of higher rewards in future steps.

However, actions like moving up or left lead the agent away from the target (out of bounds), so their Q-values will remain low.

The Q-table may look something like this:

State	Up	Down	Left	Right
(0,0)	0.00	0.75	0.00	0.75
…	…	…	…	…

How Q-learning Works?

Below are the steps of the Q-learning algorithm:

Step 1: Initialise the Q-table

To build the Q-table, you need to calculate:

The number of actions the agent can take.
The number of states of the environment, the number of potential observations the agent can return. In a grid-based environment this would be the number of cells in a grid space.

All Q-values are set to zero since the agent has no knowledge of the environment.

Step 2: Action Selection

The agent chooses an action using the epsilon-greedy method, where epsilon is used to balance exploration and exploitation. Epsilon represents the probability of taking a random action encouraging exploration, while 1 - epsilon represents the probability of selecting the action with the highest Q-value, focusing on exploitation.

At the start of training, epsilon is usually set quite high to encourage exploration. As training progresses, epsilon is decayed to encourage the agent to focus more on exploitation. However, it’s important to keep epsilon from decaying all the way to 0 to allow for occasional exploration. This will help the agent adapt to any changes to the environment.

Step 3: Agent Takes Action

The agent takes the chosen action, moves to the next state and receives feedback. This could be a reward or penalty.

Step 4: Updating Q-values

The agent updates the Q-value for the current state-action pair by considering two factors:

the immediate reward it receives for taking that action.
the maximum Q-value of the next state, the potential long-term reward.

It does this using the formula below:

\[Q_{\text{new}}(s, a) = Q_{\text{old}}(s, a) + \alpha \cdot \left( \text{reward} + \gamma \cdot \max Q(s', a') - Q_{\text{old}}(s, a) \right)\]

For me, this formula was quite confusing. So, I’ve have broken it down below in a way that helped me better understand what’s going on!

Step 5: Repeat

The agent repeats these steps until it reaches the goal and completes the task.

Formula Breakdown

The following formula is used to update the Q-values in the Q-table:

\[Q_{\text{new}}(s, a) = Q_{\text{old}}(s, a) + \alpha \cdot \left( \text{reward} + \gamma \cdot \max Q(s', a') - Q_{\text{old}}(s, a) \right)\]

\(Q_{\text{new}}(s, a)\)

The new Q-value for the state action pair \((s,a)\).

\(Q_{\text{old}}(s, a)\)

The current (old) Q-value for the state action pair \((s,a)\).

\(\alpha\)

The learning rate \(\alpha\), controls how much controls how much the agent updates its Q-value. A higher \(\alpha\) means the agent will give more weight to the most recent experience, a lower value means the agent will rely more on its past experiences. Values lie between 0 and 1:

If \(\alpha\) is close to 1, the agent quickly adjusts its Q-values but this could cause instability in learning if set too high.
If \(\alpha\) is close to 0, the agent updates its Q-values more slowly leading to more stable learning.

\(\text{reward}\)

Reward the agene receives for taking action a, referred to as immediate reward.

\(\gamma\)

The discount factor \(\gamma\) controls how much future rewards influence the agent’s action selection. Values lie between 0 and 1:

If \(\gamma\) is close to 1, the agent places more importance on long-term rewards as much as immediate rewards.
If \(\gamma\) is close to 0, the agent places less importance on long-term rewards and focuses more on immediate rewards.

\(\max Q(s', a')\)

The maximum Q-value out of all possible actions available from the next state.

In Q-learning the assumption is made that the agent will choose the best possible action in the future in order to maximise its reward.

Error Term: \(\alpha \cdot \left( \text{reward} + \gamma \cdot \max_{a'} Q(s', a') - Q_{\text{old}}(s, a) \right)\)

We can think of this like an error term, it shows the difference between the new value of Q-value and old Q-value and we use this to update the old Q-value:

if the values is positive then this means the current q-value of state s and action a is too low.
if the values is negative then this means the current q-value of state s and action a is too high.

Implementing Q-learning

Before diving into the implementation of Q-learning, I thought it would be best to first explain the reasoning behind the parameter values I’ve selected:

Learning Rate (alpha) = 0.05

A smaller learning rate of 0.05, ensures that the agent doesn’t update its values too drastically. This allows for more gradual learning, preventing the agent from overreacting to a single observation.

Discount Factor (gamma) = 0.99

The discount factor of 0.99 means the agent heavily values future rewards, encouraging it to consider long-term rewards when making decisions.

Epsilon = 1.0

Starting with an epsilon value of 1.0 ensures that the agent explores its environment fully at the beginning of the training. Since the agent has no prior knowledge of the environment, it must explore to gather information. Over time, epsilon decays shifting the agent’s behaviour to exploiting its learned Q-values.

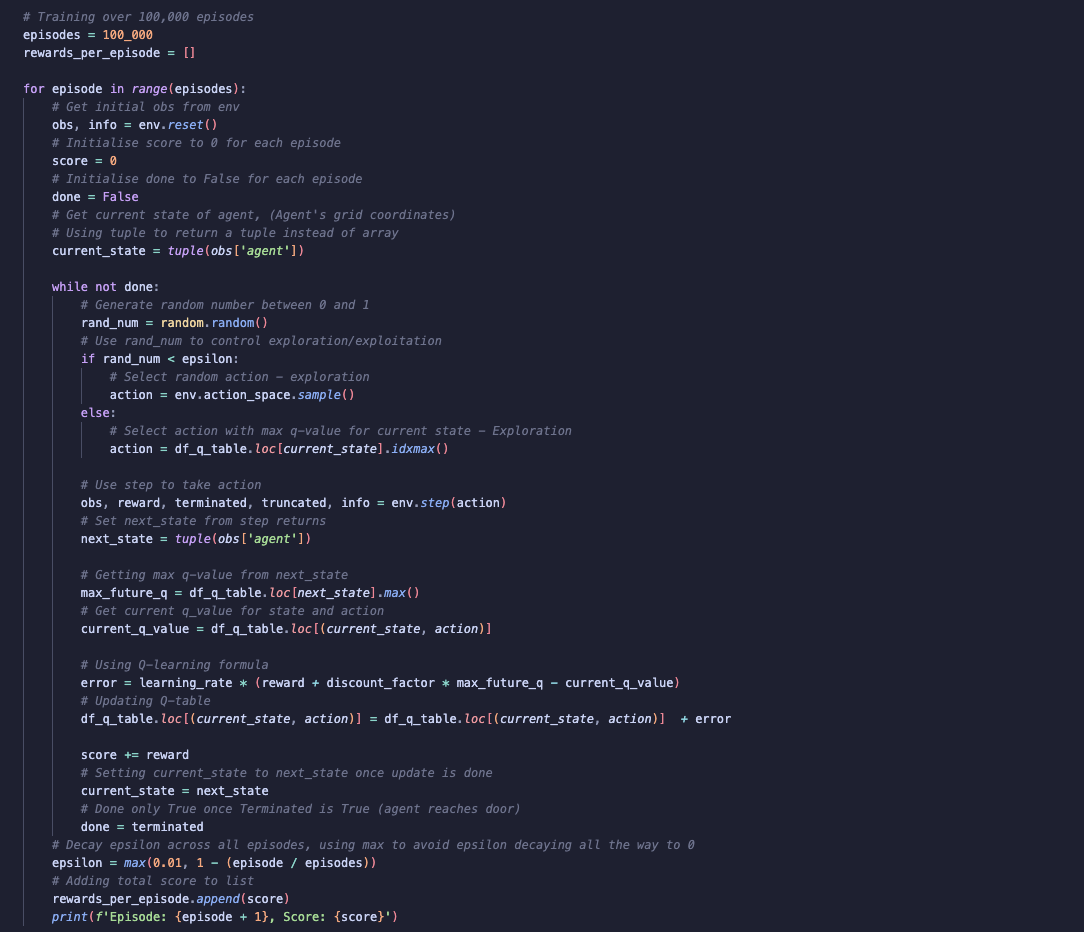
Below is a code snippet showing how I implemented Q-learning for this project. The comments in the code highlight each step of the process.

Setting up Q-Table:

Following code shows how to set up and initialise Q-Table to zeros:

Q-learning Algorithm:

Evaluation

Rewards in Training

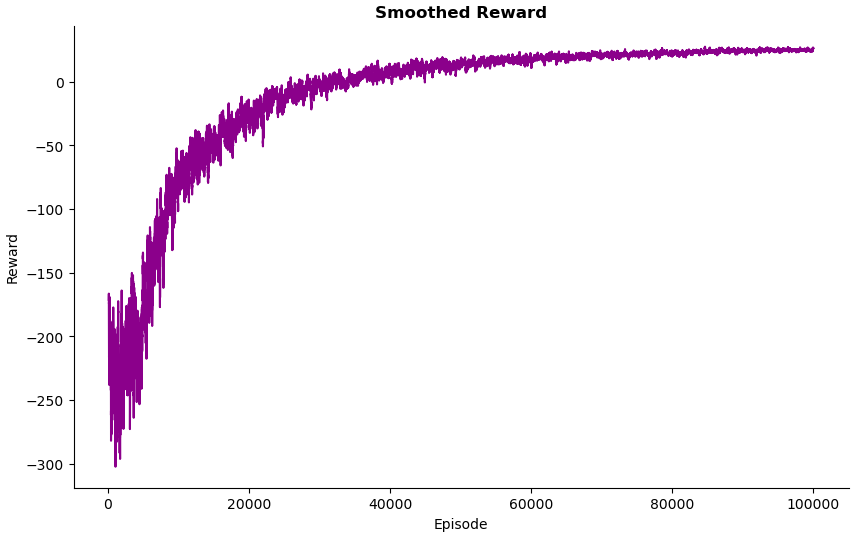
Overall, the trend shows an improvement in the agent’s performance across episodes as training progresses. This is likely due to the shift from exploration to exploitation as epsilon decays. Early in training, the agent explores randomly, leading to high variability in rewards and large penalties. As training progresses, the agent starts exploiting its learned Q-values, resulting in higher rewards. Towards the end of training, the agent’s performance starts to plateau as fewer updates are made to the Q-table, and it begins to converge.

Despite these improvements, there is still significant noise throughout training. While the rewards stabilise over time, they never fully smooth out. This is likely because epsilon is never fully decayed, meaning the agent continues to take some random actions.

Q-Table Post-Training

To understand and ensure the agent has correctly identified rewards and penalties, let’s take a look at the Q-table after training. To do this, I will take a look at the Q-values for coordinates surrounding all rewards/penalties to see what action the most likely is to take.

To make things easier to visualise, below is an image of the environment labelled with grid coordinates. I have also only included states surronding rewards/penalties, for the full Q-table please visit the notebooks on my GitHub.

Q-Table

x,y	Right	Down	Left	Up
1, 2	898.339397	853.946836	851.868359	844.924496
1, 4	826.755382	833.318023	816.587151	882.851914
2, 0	889.013584	852.770221	836.772617	844.737672
2, 1	829.508097	896.996317	824.613841	826.097483
2, 3	901.587616	853.005231	856.767189	871.075641
3, 1	851.459695	892.505529	868.825547	860.689521
3, 2	862.197133	901.773882	879.004504	869.598686
3, 4	920.452735	901.876677	866.197932	891.033779
4, 0	814.447182	819.636694	887.955279	820.563501
4, 1	814.995657	820.727337	882.425660	820.630816
4, 3	870.760765	919.599819	861.267063	839.077761

Environment:

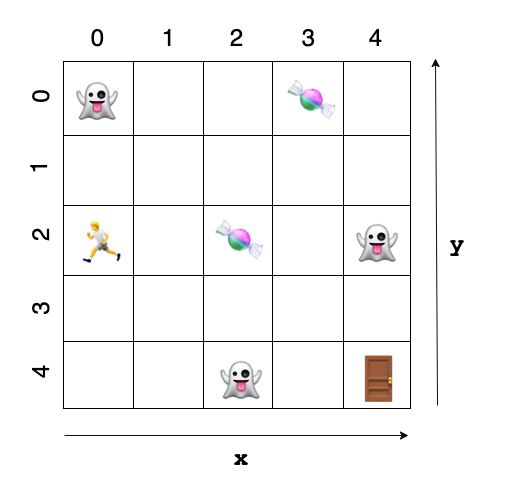
(4, 4) Exit Door [+20]

The exit door is the largest reward in the environment and the agent should have learnt to prioritise this location.

(4,3): The highest Q-value is for moving Down. This makes sense since moving down brings the agent closer to the exit.
(3,4): The highest Q-value is for the Right action, reflecting the path towards the exit at (4,4).

(4, 2) Ghost 1 [-25]

The agent must learn to avoid ghosts as an encounter with a ghost results in a penalty of -25.

(4,1): The highest Q-valueis for moving Left, indicating that the agent has learned to avoid the ghost at (4,2) by stepping left.
(3,2): The highest Q-value is for moving Down, leading towards the exit door, suggesting that the agent prefers to avoid the ghost and head towards the reward.

(2, 4) Ghost 2 [-25]

Similarly, the agent needs to avoid the second ghost.

(1,4): The highest Q-value is for moving Up, showing that the agent knows to avoid the ghost at (2,4) by moving upward.
(2,3): The highest Q-value is for moving Left, towards the exit door, demonstrating the agent’s understanding of prioritising rewards over penalties.

(2, 2) Candy 1 [+15]

The agent learns to collect candies, which provide a smaller but valuable reward.

(2,1): The highest Q-value is for moving Down, which is a path that leads towards the candy at (2,2).
(1,2): The highest Q-value is for moving Right, indicating that the agent learns to move towards the candy.
(3,2): Interestingly, the agent looks ahead, favouring the Down action to move towards the exit door instead of staying to collect the candy. This shows the agent is learning to balance immediate rewards with long-term goals.
(2,3): The highest Q-value is for moving Right, as it leads towards the exit, while the second-highest Q-value is Up, suggesting the agent still values the candy.

(3, 0) Candy 2 [+15]

Another candy that the agent must learn to collect while also keeping an eye on the long-term goal.

(2,0): The highest Q-value is for Right. The agent has successfully learned to collect the candy from this state. The second-highest Q-value is Down towards the door.
(4,0): The highest Q-value is for moving Left, meaning the agent has learned to collect the candy at (3,0).
(3,1): The highest Q-value is for moving Down, reinforcing the idea that the agent is focusing on reaching the exit.

Testing

In the video, you can see the agent’s actions and see how the Q-values discussed above influences its decisions!

From observing the agent in the environment post-training, the agent is performing as expected. The main objective is for the agent to reach the exit door and avoid the ghosts. If there are candies on the way, the agent should collect them but the main priority is to reach the exit door.

Possible Improvements

Two things I could have done to further improve on this RL:

Incorporating the location of candies and ghosts:

Including the agent’s distance to candies and ghosts in the training could allow for smarter decisions and behaviour.

Increasing Reward for Collecting More Candies:

Increasing the reward for each additional candy the agent collects could incentivise the agent to collect more candies. While this was outside of the scope of the original project, it could be something worth adding as I progress to the final environment (Phase 3).

Summary

In this post, I have discussed steps I took to expand on the first iteration of my custom environment by adding in ghosts and candies. The objective of the agent expanded to not only successfully reach the exit door but also avoid ghosts and collect candies. I also introduced Q-learning and explained how I used the algorithm to train my agent by considering both immediate and long-term rewards.

To see the full code and additional comments, this follow this link to my GitHub and navigate to the Trick Or ReTreat repo (to be made public on completing the project)!